Note

You can download this example as a Jupyter notebook or start it in interactive mode.

Use Coordinates

Now, the real power of the package comes into play!

Linopy is structured around the concept that variables, and therefore expressions and constraints, have coordinates. That is, a Variable object actually contains multiple variables across dimensions, just as we know it from a numpy array or a pandas.DataFrame.

Suppose the two variables x and y are now functions of time t and we would modify the problem according to:

Minimize:

\[\sum_t x_t + 2 y_t\]

subject to:

\[\begin{split}x_t \ge 0 \qquad \forall t \\ y_t \ge 0 \qquad \forall t \\ 3x_t + 7y_t \ge 10 t \qquad \forall t\\ 5x_t + 2y_t \ge 3 t \qquad \forall t\end{split}\]

whereas t spans all the range from 0 to 10.

In order to formulate the new problem with linopy, we start again by initializing a model.

import linopy

m = linopy.Model()

Again, we define x and y using the add_variables function, but now we are adding a coords argument. This automatically creates optimization variables for all coordinates, in this case time-steps.

import pandas as pd
time = pd.Index(range(10), name='time')

x = m.add_variables(lower=0, coords=[time], name='x', )
y = m.add_variables(lower=0, coords=[time], name='y')

Following the previous example, we write the constraints out using the syntax from above, while multiplying the rhs with t. Note that the coordinates from the lhs and the rhs have to match.

Note

In the beginning, it is recommended to use explicit dimension names. Like that, things remain clear and no unexpected broadcasting (which we show later) will happen.

factor = pd.Series(time, index=time)

3*x + 7*y >= 10*factor

Constraint (unassigned) (time: 10):
-----------------------------------
[0]: +3 x[0] + 7 y[0] ≥ -0.0
[1]: +3 x[1] + 7 y[1] ≥ 10.0
[2]: +3 x[2] + 7 y[2] ≥ 20.0
[3]: +3 x[3] + 7 y[3] ≥ 30.0
[4]: +3 x[4] + 7 y[4] ≥ 40.0
[5]: +3 x[5] + 7 y[5] ≥ 50.0
[6]: +3 x[6] + 7 y[6] ≥ 60.0
[7]: +3 x[7] + 7 y[7] ≥ 70.0
[8]: +3 x[8] + 7 y[8] ≥ 80.0
[9]: +3 x[9] + 7 y[9] ≥ 90.0

It always helps to write out the constraints before adding them to the model. Since they look good, let’s assign them.

con1 = m.add_constraints(3*x + 7*y >= 10*factor, name='con1')
con2 = m.add_constraints(5*x + 2*y >= 3*factor, name='con2')
m

Linopy LP model
===============

Variables:
----------
 * x (time)
 * y (time)

Constraints:
------------
 * con1 (time)
 * con2 (time)

Status:
-------
initialized

Now, when it comes to the objective, we use the sum function of linopy.LinearExpression. This stacks all terms all terms of the time dimension and writes them into one big expression.

obj = (x + 2*y).sum()
m.add_objective(obj)

m.solve()

Restricted license - for non-production use only - expires 2025-11-24

Read LP format model from file /tmp/linopy-problem-6uapdwd9.lp

Reading time = 0.00 seconds

obj: 20 rows, 20 columns, 40 nonzeros

Gurobi Optimizer version 11.0.1 build v11.0.1rc0 (linux64 - "Ubuntu 22.04.3 LTS")

CPU model: Intel(R) Xeon(R) Platinum 8259CL CPU @ 2.50GHz, instruction set [SSE2|AVX|AVX2|AVX512]

Thread count: 1 physical cores, 2 logical processors, using up to 2 threads

Optimize a model with 20 rows, 20 columns and 40 nonzeros

Model fingerprint: 0x3434cd3b

Coefficient statistics:

  Matrix range     [2e+00, 7e+00]

  Objective range  [1e+00, 2e+00]

  Bounds range     [0e+00, 0e+00]

  RHS range        [3e+00, 9e+01]

Presolve removed 2 rows and 2 columns

Presolve time: 0.01s

Presolved: 18 rows, 18 columns, 36 nonzeros

Iteration    Objective       Primal Inf.    Dual Inf.      Time

       0    0.0000000e+00   7.312500e+01   0.000000e+00      0s

      18    1.2879310e+02   0.000000e+00   0.000000e+00      0s

Solved in 18 iterations and 0.01 seconds (0.00 work units)

Optimal objective  1.287931034e+02

('ok', 'optimal')

In order to inspect the solution. You can go via the variables, i.e. y.solution or via the solution aggregator of the model, which combines the solution of all variables. This can sometimes be helpful.

m.solution.to_dataframe().plot(grid=True, ylabel='Optimal Value');

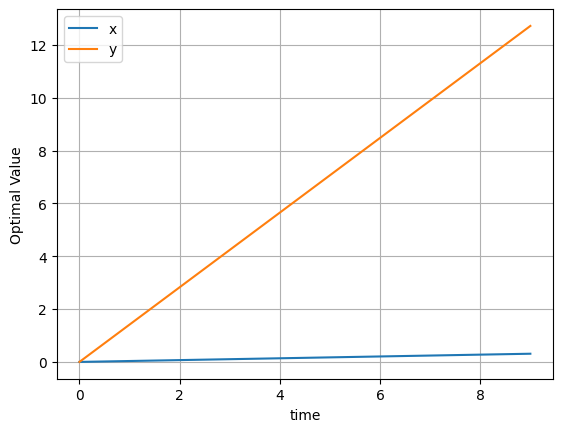
Alright! Now you learned how to set up linopy variables and expressions with coordinates. In the User Guide, which follows, we are going to see, how the representation of variables with coordinates allows us to formulate more advanced operations.